线段树优化建图

Coding, OI, 精选文章！ , 5 Comments

感觉挺好玩的就写一个。

例题：CF786B

题目大意是，给定 q 次操作，有 3 种：

  1. 连边 u\to v
  2. 连边 u \to [l, r]
  3. 连边 [l, r] \to u

然后要跑一个最短路。那么很显然的是，如果你暴力建边，时间复杂度 O(nq) 显然会超时。那么这个时候可以考虑线段树优化建边。

拿有 5 个节点的图举例子。

先来说怎么做。

首先，显然，你需要一棵线段树。

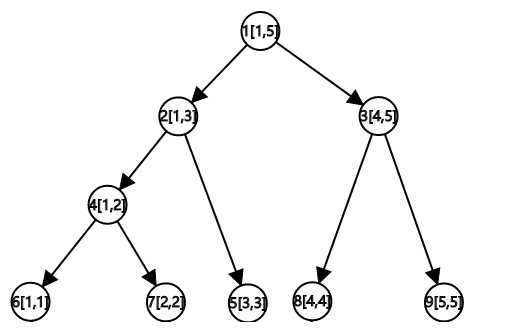
你需要根据这棵线段树的 父子关系 来建边，并且权值为 0。

上树（入树）可以保证你可以从任意 区间 走到任意的 点。

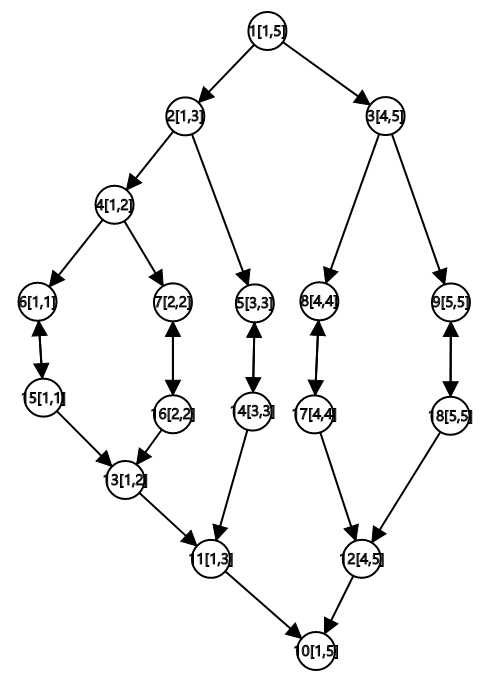
然后再开一棵线段树，从儿子指向父亲建边。

下树（出树）可以保证你可以从任意的 点 走到任意 区间。

（注意：这里的建边和线段树的操作是独立的。线段树只需要维护左区间和右区间端点即可。）

然后，你需要把两棵线段树的叶子节点用双向边连起来，因为它们本来就是一个点。

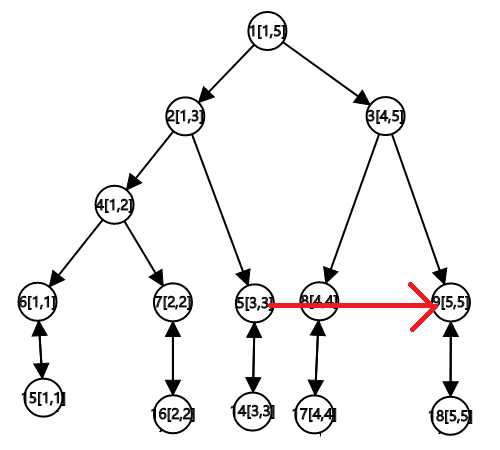
对于操作 1，即点连点，直接在图上操作即可。建在上树（出树）的叶子节点和下树（入树）的叶子节点无所谓，因为两棵树的对应叶子节点连边后成为了一个 强连通分量，相互可达，所以这是无所谓的。

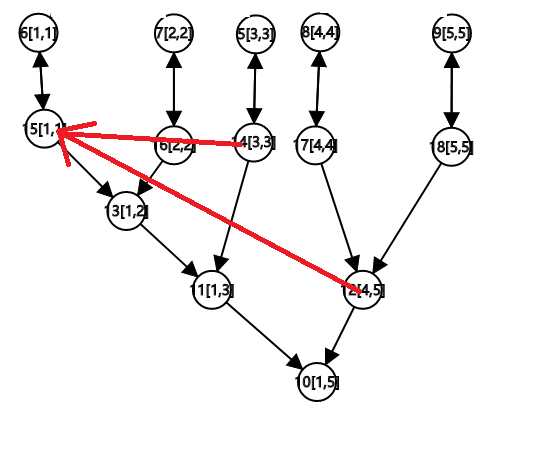
例子：建边 3 \to 5

（不涉及到树的操作，因此下树略）

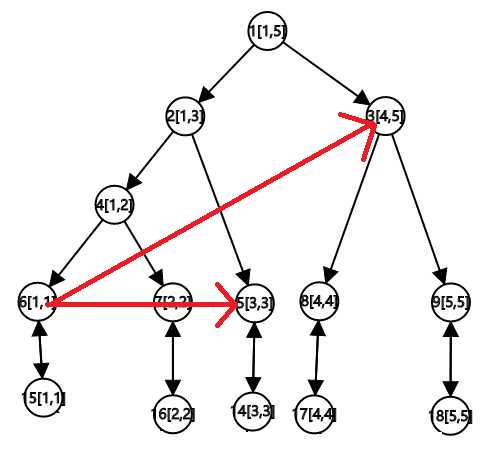
操作 2，即点连区间。观察到上树可以从区间走到点，因此考虑这样一条路径：点→区间→点。那么从叶子节点向上树建边即可。

通过线段树分治连边。

例子：建边 1\to [3, 5]

操作 3，区间连点。考虑这样一条路径：区间→点（→其它区间/点）。那么把下树和对应叶子节点连起来就行。

例子：建边 [3, 5]\to 1

然后没了。

我知道有入树和出树的说法，但是感觉这样的说法（在本文）不便形象理解。但是你会了其实都无所谓。

我这儿用了一个有点动态的写法。

核心代码：

int node_cnt = 0;
inline int alloc_node() { return ++node_cnt; }

void build(int l, int r, int root, int direction)
{
    nd[root].l = l; nd[root].r = r;
    if (l == r) {
        // 标记叶子节点位置
        flag[direction][l] = root;
        return;
    }
    nd[root].lson = alloc_node();
    nd[root].rson = alloc_node();
    // addedge
    if (direction == 0) {
        // 上 -> 下
        addedge(root, nd[root].lson, 0);
        addedge(root, nd[root].rson, 0);
    } else {
        // 下 -> 上
        addedge(nd[root].lson, root, 0);
        addedge(nd[root].rson, root, 0);
    }
    int mid = (l + r) >> 1;
    build(l, mid, nd[root].lson, direction);
    build(mid + 1, r, nd[root].rson, direction);
}

// p -> [l, r]
// In Tree (direction = 0)
void point_to_range(int p, int l, int r, long long w, int root)
{
    if (r < nd[root].l || nd[root].r < l) return;
    if (l <= nd[root].l && nd[root].r <= r) {
        addedge(flag[0][p], root, w);
        return;
    }
    point_to_range(p, l, r, w, nd[root].lson);
    point_to_range(p, l, r, w, nd[root].rson);
}

// [l, r] -> p
// Out Tree (direction = 1)
void range_to_point(int l, int r, int p, long long w, int root)
{
    if (r < nd[root].l || nd[root].r < l) return;
    if (l <= nd[root].l && nd[root].r <= r) {
        addedge(root, flag[0][p], w);
        return;
    }
    range_to_point(l, r, p, w, nd[root].lson);
    range_to_point(l, r, p, w, nd[root].rson);
}

int dt0, dt1;

int main()
{
    cin >> n >> q >> s;
    // 初始化上树
    dt0 = alloc_node();
    build(1, n, dt0, 0);
    // 初始化下树
    dt1 = alloc_node();
    build(1, n, dt1, 1);
    // 连叶子
    for (int i = 1; i <= n; i++) {
        addedge(flag[0][i], flag[1][i], 0);
        addedge(flag[1][i], flag[0][i], 0);
    }
    // 中间略
    // 这只是一个 **普通** 最短路板子
    Dij(flag[0][s]);
    // 输出略
    return 0;
}

练习题：P6348 [PA2011] Journeys

写得比较用心的水文。