「大概是题解」HDU 3333 Turing Tree / HH 的项链

其实一开始写这玩意是因为感觉自己 lambda 写得很好看（

HDU 3333 Turing Tree

link

aka 「HH 的项链」，但是维护的东西不一样，题意也有一些细微的差别。

题目大意是说，有 Q 次询问，每次询问查询区间 [l, r] 之间不重复的数字之和。没有修改操作。

既然没有修改那不是离线然后乱搞（

考虑离线对所有询问以区间右端点为关键字进行升序排序。然后从左到右遍历数据。

见图。上面一行是线段树的更改，下面的是数据。

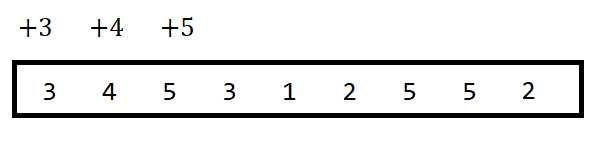
记录一个 \text{last} _ i，用来表示上次 i 出现的位置。

这个时候注意到 3 在线段树中出现过了。这个时候，只用把原来位置减去 3，再在现在的位置加上 3，确保这个 3 在当前区间的查询中只被计算一次。

查询的话，只用查询 [l, r] 的区间和就行了。

实现上的细节就是注意多测清空，然后 \text{last} 要开 map，因为值域最大 1\times 10^9。

据说这玩意还可以分块乱搞。不会。

Code:

cin >> n;
for (int i = 1; i <= n; i++) cin >> dat[i];
cin >> k;
for (int i = 1; i <= k; i++) {
    cin >> queries[i].l >> queries[i].r;
    queries[i].id = i;
}
lastans.clear();
tree.build(1, n);
sort(queries + 1, queries + 1 + k,
    [](const Query x, const Query y) {
        if (x.r == y.r) return x.l < y.l;
        else return x.r < y.r;
    }
);
int lastr = 1;
for (int i = 1; i <= k; i++) {
    for (; lastr <= queries[i].r; lastr++) {
        if (lastans[dat[lastr]]) {
            // 减去原来的
            tree.update_nodes(
                lastans[dat[lastr]],
                lastans[dat[lastr]],
                -dat[lastr]
            );
        }
        // 记录
        lastans[dat[lastr]] = lastr;
        // 加上现在的
        tree.update_nodes(
            lastr,
            lastr,
            dat[lastr]
        );
    }
    queries[i].ans = tree.query(queries[i].l, queries[i].r);
}
sort(queries + 1, queries + 1 + k,
    [](const Query x, const Query y) {
        return x.id < y.id;
    }
);
for (int i = 1; i <= k; i++) {
    cout << queries[i].ans << '\n';
}