树状数组离线 修&查 二维二阶前缀和
感觉是一个很多人用的,但是搜了一圈好像没人写(
首先是一道题。校内模拟赛的,不知道有没有原(
在 n \times m 的平面上有 n 个互不相交的矩形(可以看作平面直角坐标系),左下角为 (x_1, y_1),右上角为 (x_2, y_2)。然后有 q 组询问,每次询问查询给定矩形与平面上每个矩形的面积交的和。
n, m \le 5\times 10^5。
有一个朴素的 O(nm) 的做法,就是差分维护给定的矩形(修改),跑两遍前缀和,第一遍前缀和求出差分数组的原数组,第二遍是为了快速区间求和,最后 O(1) 查询即可。
然后,你会发现,这就是一个二维树状数组维护一个二阶的前缀和(参见树状数组维护前缀和的前缀和的「二维前缀和的前缀和」一节),但是看数据规模很明显不支持二维树状数组。
把二维树状数组维护二阶前缀和的公式抄下来了 ↓
(公式没法写 block 要不然预览越界到屏幕外面去了,建议屏幕分辨率高的开最大化)
s_{i,j} =(i+1)(j+1)\sum_{p=1}^{i} \sum_{q=1}^{j}a_{p,q}-(j+1)\sum_{p=1}^{i} \sum_{q=1}^{j}p \times a_{p,q}-(i+1)\sum_{p=1}^{i} \sum_{q=1}^{j}q \times a_{p,q}+\sum_{p=1}^{i} \sum_{q=1}^{j}pq \times a_{p,q}
这个公式成功地把一阶前缀和变成了二阶前缀和。
因为这个题只需要单点修改就可以了,所以不妨换个思路,把所有查询和操作都离线下来,然后用树状数组维护 \sum_{j=1}a_{i,j}、\sum_{j=1}i\times a_{i,j}、\sum_{j=1}j\times a_{i,j} 和 \sum_{j=1}ij\times a_{i,j} 即可。对于 i 这一维,离线下来然后暴力枚举就可以啦。i,j,a_{i,j} 怎么相乘都是定值,所以可以放心大胆维护。有点像,拿树状数组从下往上扫。
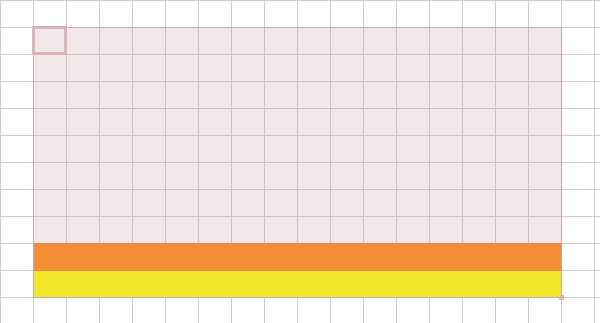
(粉色区域代表整个矩形,黄色代表维护的部分)

然后在更新的时候叠加上橙色区域的更改。
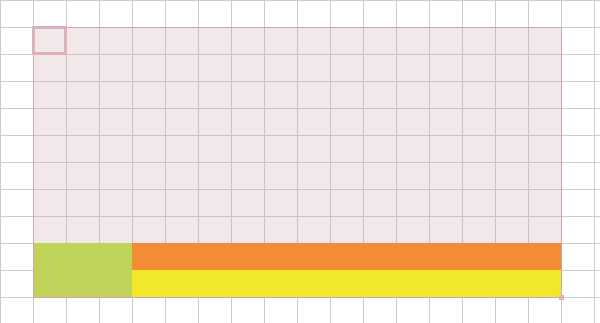
然后暴力扫的同时就相当于维护了 \sum_{i=1}^{current}\sum_{j=1} a_{i,j} 的值。(绿色区域)
然后套公式,结合四个树状数组维护的信息,你就维护了 \sum_{i=1}^{current}\sum_{j=1} a_{i,j} 的前缀和。(a_{i,j} 的二阶前缀和)
Sample Code:
// n -> w, m -> l
#include <climits>
#include <cmath>
#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
template <class T>
constexpr T lowbit(T x) { return x & -x; }
int n, m, w, l;
vector<pair<int, int>> modi[500005];
vector<pair<int, ll&>> quey[500005];
struct Query {
ll top_right, top_left, bot_right, bot_left;
} qr[500005];
struct BIT {
ll dat[500005];
inline void add(int pos, ll d)
{
for (; pos <= l; pos += lowbit(pos))
dat[pos] += d;
}
inline ll query(int pos)
{
ll res = 0;
for (; pos > 0; pos -= lowbit(pos))
res += dat[pos];
return res;
}
} tr1, tr2, tr3, tr4;
int main()
{
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int n, q;
cin >> n >> q;
cin >> w >> l;
// 先修再查
int tx1, ty1, tx2, ty2;
for (int i = 1; i <= n; i++) {
cin >> tx1 >> ty1 >> tx2 >> ty2;
// 边界修正
tx2++, ty2++;
tx1++, ty1++;
modi[tx1].push_back({ ty1, 1 });
modi[tx1].push_back({ ty2, -1 });
modi[tx2].push_back({ ty1, -1 });
modi[tx2].push_back({ ty2, 1 });
}
for (int i = 1; i <= q; i++) {
cin >> tx1 >> ty1 >> tx2 >> ty2;
quey[tx1].push_back({ ty1, qr[i].bot_left });
quey[tx1].push_back({ ty2, qr[i].top_left });
quey[tx2].push_back({ ty1, qr[i].bot_right });
quey[tx2].push_back({ ty2, qr[i].top_right });
}
for (int i = 1; i <= w; i++) {
for (auto [j, d] : modi[i]) {
tr1.add(j, d);
tr2.add(j, 1ll * i * d);
tr3.add(j, 1ll * j * d);
tr4.add(j, 1ll * i * j * d);
}
for (auto& [j, val] : quey[i]) {
val = 1ll * (i + 1) * (j + 1) * tr1.query(j)
- 1ll * (j + 1) * tr2.query(j)
- 1ll * (i + 1) * tr3.query(j)
+ 1ll * tr4.query(j);
}
}
for (int i = 1; i <= q; i++)
cout << qr[i].top_right - qr[i].top_left - qr[i].bot_right + qr[i].bot_left << '\n';
}