非常有意思的一道找规律数据结构简单题（存疑，CF1862G）

OI, 题解 , , 0 Comments

CF Link | Luogu Link

昨天比赛写的一道非常有意思的题，完赛前 5 分钟想出的解法（然后没写出来）。

主要讲的是找规律，然后没有很严谨的数学证明。

题意

定义一个对序列的操作为：

  1. 升序排序 + 去重
  2. 如果只剩一个元素就返回这个元素
  3. 将所有元素 a_i（下标从 0 开始）加上 n – i，并回到步骤 1。

有 q 次询问，每次询问修改原序列上下标为 i 的一个数，在每次修改后求出这个新序列的操作值。

解法

找规律。如果数感好并且想象力比较丰富的话，可以大概看出来一些规律。

原序列的顺序对操作结果没有影响，所以这里把样例升序排序。就拿题目给定的样例解释看：

[4, 6, 8] -> 10
[6, 8, 10] -> 12
[1, 6, 10] -> 15

排序之后，应该不难看出序列到结果的一个规律：

结果 = 原序列最大值 + 排序后某连续两个数的差值

比方说，拿 [1, 6, 10] \to 15 举例：15 = 10 + (6 – 1)

到底是哪两个数的差值可以写一个暴力来进一步找规律。

void bruteforce()
{
    int n = 3;
    vector<int> arr(n);
    for (auto &x : arr) cin >> x;
    while (arr.size()) {
        sort(arr.begin(), arr.end());
        arr.erase(unique(arr.begin(), arr.end()), arr.end());
        if (arr.size() == 1) {
            cout << arr[0] << endl;
            return;
        }
        for (int i = 0; i < arr.size(); i++) {
            arr[i] += n - i;
        }
    }
}

手构几组数据，应该不难看出，这个差值是最大的连续两个数的差值。

这个时候解法就出来了。可以用一个 multiset 维护序列内的数值（可以通过寻找前驱/后继来动态更新排序后相邻元素的差值），再用另一个 multiset 维护排序后相邻元素的差值。

修改时具体操作捋一下，就几个：

  1. 从维护数值的 multiset 里寻找到旧的 x 的前驱和后继；
  2. 从维护差值的 multiset 里删除旧的 x 和它的前驱/后继的差值，插入其前驱与后继的差；
  3. 删除旧的 x，插入新的 x；
  4. 在维护差值的 multiset 里插入新的 x 与它前驱/后继的差值，删除前驱后继的差。

画个图就是这样：

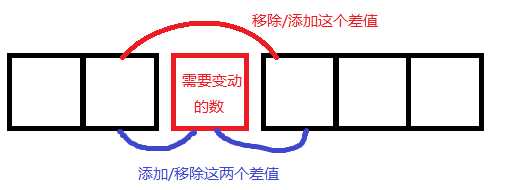
最后再注意一下边界条件就可以做出来了。

Code:

// mt 存值，sp 存差值
multiset<int> mt, sp;

inline void solve()
{
    mt.clear(); sp.clear();
    i64 n;
    cin >> n;
    // 特判，否则会 RE
    if (n == 1) sp.insert(0);
    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        mt.insert(s[i]);
    }
    auto it = mt.begin();
    int last = *(it++);
    while (it != mt.end()) {
        sp.insert(*it - last);
        last = *(it++);
    }
    cin >> q;
    while (q--) {
        cin >> x >> v;
        // find s[x] and unbind
        auto it = mt.find(s[x]);
        int beg = -1, end = -1;
        // has pre
        if (it != mt.begin()) {
            auto rit = it--;
            beg = *it;
            sp.erase(sp.find(*rit - *it));
            it++;
        }
        // has nxt
        auto lit = it++;
        if (it != mt.end()) {
            sp.erase(sp.find(*it - *lit));
            end = *it;
        }
        mt.erase(lit);
        // has pre and nxt
        if (beg != -1 && end != -1) {
            sp.insert(end - beg);
        }
        // insert v and bind
        beg = -1; end = -1;
        s[x] = v;
        it = mt.insert(s[x]);
        // has pre
        if (it != mt.begin()) {
            auto rit = it--;
            beg = *it;
            sp.insert(*rit - *it);
            it++;
        }
        // has nxt
        lit = it++;
        if (it != mt.end()) {
            sp.insert(*it - *lit);
            end = *it;
        }
        // has pre and nxt
        if (beg != -1 && end != -1) {
            sp.erase(sp.find(end - beg));
        }
        cout << *sp.rbegin() + *mt.rbegin() << ' ';
    }
    cout << '\n';
}